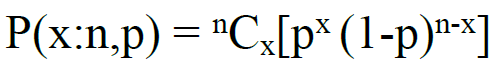Picking a sample size for CAPA or FAI
This is the first in a series I might end up calling “Google Couldn’t Tell Me How To Do This” (GCTMHTDT). It will be reserved for tasks a quality engineer or related role might have to do regularly but there is surprisingly no accepted method online or in the applicable standards. Of course this comes with the caveat that I’m just one person, so if you have a different way of doing it or a good reference that I missed, drop it in the comments. Now to the topic…
INSPECTION is one of those ubiquitous tasks in the world of med device design and manufacture that no one seems to love. In fact it has been a significant achievement in the development of 20th century quality management to reduce reliance on manual inspection as much as possible through the use of process design tools such as P-FMEA and IQ/OQ/PQ. Statistical methods now captured in standards such as the ISO 2859 family also help us greatly reduce the burden of inspection by telling us the minimum sample sizes to inspect to ensure certain acceptable quality limits (AQL) are being reached. This family of standards requires a pre-determined “population” to draw a sample from. This population is a production lot; all of the methods in the ISO 2859 standards are designed for lot-based inspection, either singular or continuous. This works well for an ongoing production inspection, where the business decides what lot size to produce and hands each lot off to the inspector, who can then plug the lot size into the appropriate AQL or LQ table from ISO 2859 and get their sample size spit out.
But not all inspections have a pre-determined lot size. For example, your company has designed a new medical device and is ready to qualify its production line. Part of this qualification is First Article Inspection (FAI), where a special lot of units is produced for the purposes of a special inspection to catch any remaining issues and ensure the line is ready to go. Since the FAI lot size is not pre-determined, and in fact is entirely up to you as the quality engineer, ISO 2859 won’t be much help. There is no pre-determined population to draw a sample from. So how do you decide what the FAI lot size should be?
The binomial probability distribution method for FAI
In my mind, the best method is using the binomial probability distribution. The binomial distribution formula can be used to determine the probability P that x number of successes will occur given n number of trials are conducted when the probability of success in a single trial is p. The formula is as follows:
A First Article Inspection can be characterized as a binomial probability distribution experiment because the outcomes in the inspection are success or failure. Although the wording is counterintuitive, in the case of a First Article Inspection, we will consider a “success” to be the detection of a defect in a single unit. Each unit in the inspection lot has a chance of either having a defect (success) or not having a defect (failure). If we can input P, x, and p, we will be able to calculate n to determine the proper lot size for our inspection.
Before we set our variables, we should mention that it is not possible to directly calculate the n number of trials required to find at least one existing defect. In statistics it is a common method to indirectly calculate the probability of at least one success by calculating the probability of the opposite situation (zero successes) and then subtracting that result from 1. Now let’s set the variables:
For P: If we want a 95% chance that we will find at least one existing defect, we will set P to 5% (0.05) as the probability that zero defects are found.
For x: Since we are using a P of 5% as the probability that zero defects are found, we likewise will want to set the number of successes x to 0.
For p: We can set a very low probability of occurrence of the defect to ensure FAI is sufficiently rigorous. In this case, we will set p to 3% (0.03).
Now we can solve for n:
We see above that having 99 units in our inspection lot will result in a 5% chance that we will find 0 defects given a defect probability of 3%, or in other words, a 95% chance that we will find at least 1 defect given a defect probability of 3%. Increasing n will increase the probability closer to 100%. For example, if we set n to 150, we will end up with ~1% chance that 0 defects will be found, or 99% chance that at least 1 defect will be found. A binomial calculator may be used to experiment with different lot sizes, rather than manual calculation using the formula above. The experiment is also visualized in the graph below:
X axis = binomial probability of at least 1 defect being found given a 3% probability of occurrence, Y axis = number of trials (lot size)
Alternatives to the binomial distribution method for FAI
I am by no means an expert on this topic, but I will list some alternative methods I have seen and what I think their downsides are:
I have seen lot sizes chosen based on the planned size of a typical production lot. While this sounds good in theory, in practice, if the planned production lot sizes are very large, you are investing a much larger amount of money into building the lot than statistically required. If there is an defect present, then reworking the lot or building another lot for a second qualification just adds to those costs.
I have also seen some manufacturers simply run FAI on the first production lot, instead of building a special qualification lot. The downside is that some auditors and internal quality managers are squeamish with the concept of allowing qualification units to be used in the field by real end users, since they are technically part of the “pre-production” process and have been handled in ways not accounted for in the Device Master Record (for example, in manufacturing work instructions). However, this is the “leanest” option and I think should be considered if the device risk is sufficiently low and if manufacturing costs are high.
Application of binomial probability distribution for CAPA
One other application I have found for this method is deciding a sample size for CAPA effectiveness checks. Auditors often press on whether the CAPA writer has valid statistical rationale for the quantity of samples to evaluate in the effectiveness check phase, particularly when the audit criteria include FDA 21 CFR 820 Subpart J. They want to make sure that the check really does prove that the actions were correct. Using the binomial distribution method specified above gives you rationale to show that the sample size chosen results in a quantifiably high probability that any lingering defects will be found. Of course, not every CAPA involves an effectiveness check on a discrete quantity of units, but in many cases it is applicable.